1)Statistical Process Control (SPC) [Group: Management system]
[old]
Statistical process control (SPC) is the application of statistical methods to the monitoring and control of a process to ensure that it operates at its full potential to produce conforming product. Under SPC, a process behaves predictably to produce as much conforming product as possible with the least possible waste. While SPC has been applied most frequently to controlling manufacturing lines, it applies equally well to any process with a measurable output. Key tools in SPC are control charts, a focus on continuous improvement and designed experiments.Much of the power of SPC lies in the ability to examine a process and the sources of variation in that process using tools that give weight to objective analysis over subjective opinions and that allow the strength of each source to be determined numerically. Variations in the process that may affect the quality of the end product or service can be detected and corrected, thus reducing waste as well as the likelihood that problems will be passed on to the customer. With its emphasis on early detection and prevention of problems, SPC has a distinct advantage over other quality methods, such as inspection, that apply resources to detecting and correcting problems after they have occurred.
In addition to reducing waste, SPC can lead to a reduction in the time required to produce the product or service from end to end. This is partially due to a diminished likelihood that the final product will have to be reworked, but it may also result from using SPC data to identify bottlenecks, wait times, and other sources of delays within the process. Process cycle time reductions coupled with improvements in yield have made SPC a valuable tool from both a cost reduction and a customer satisfaction standpoint.
[old]
Statistical process control (SPC) is the application of statistical methods to the monitoring and control of a process to ensure that it operates at its full potential to produce conforming product. Under SPC, a process behaves predictably to produce as much conforming product as possible with the least possible waste. While SPC has been applied most frequently to controlling manufacturing lines, it applies equally well to any process with a measurable output. Key tools in SPC are control charts, a focus on continuous improvement and designed experiments.Much of the power of SPC lies in the ability to examine a process and the sources of variation in that process using tools that give weight to objective analysis over subjective opinions and that allow the strength of each source to be determined numerically. Variations in the process that may affect the quality of the end product or service can be detected and corrected, thus reducing waste as well as the likelihood that problems will be passed on to the customer. With its emphasis on early detection and prevention of problems, SPC has a distinct advantage over other quality methods, such as inspection, that apply resources to detecting and correcting problems after they have occurred.
In addition to reducing waste, SPC can lead to a reduction in the time required to produce the product or service from end to end. This is partially due to a diminished likelihood that the final product will have to be reworked, but it may also result from using SPC data to identify bottlenecks, wait times, and other sources of delays within the process. Process cycle time reductions coupled with improvements in yield have made SPC a valuable tool from both a cost reduction and a customer satisfaction standpoint.
[New][Better]
Statiscal process control (SPC) began as a means of controlling production in a manufacturing plant. It soon became obvious that SPC principles could be extended into other areas, such as nonmanufacturing (areas other than production in a manufacturing firm, and all areas of a service-type industry), management, health care, education, politics, the family, and even life itself.
SPC is a system of management: one that concentrates on quality rather than on productivity or accounting ( as used to be the case in the past, and still is in many firms). A quality management system concentrates on the sustomer while the old productivity/accounting management system appears to concentrate on things (how many and/ how much).
(Statistical process control, Leonard A. Doty, 1996, pp.2-3)
2)Statistical Quality Control [Group: Quality control]
[Old]
Statistical Quality Control is a set of techniques intended to aid in the improvement of system quality. Statistical Quality Control(SQC) refers to the application of statistical methods to monitor and evaluate systems and to determine whether changing key input variable (KIV) settings is appropriate. Specifically, SQC is associated with Shewhart’s statistical process charting (SPC) methods. These SPC methods include several charting procedures for visually evaluating the consistency of key process outputs (KOVs) and identifying unusual circumstances that might merit attention. In common usage, however, SQC refers to many problem-solving methods. Some of these methods do not relate to monitoring or controlling processes and do not involve complicated statistical theory. In many places, SQC has become associated with all of the statistics and optimization methods that professionals use in quality improvement projects and in their other job functions. This includes methods for design of experiments (DOE) and optimization.
(Introduction to Engineering Statistics and Six Sigma, Theodore T. Allen; Page: 29)
[New][Better]
The quality of a product is the most important property that one desires while purchasing it. A product is of good quality, if it meets the required specifications, otherwise not. In this competitive world, the succuss of a manufacturer mostly depend on quality of his product. Also, the quality of the product should be maintained so that the reputation of the company does suffer. The quality of every product or article can be defined, but statistical quality control deals with the quality of the articles produced in an industry. It is commonly felt that all the articles produced by a machine will be exactly similar, but this is not true as variation is inherent an unavoidable. On taking measurements pertaining to certain characteristics of articles, it is found that they do differ from one another. If this difference is negligible from the desired measurements, the article is acceptable and if it differs much from the specifications, it is to be rejected.
A manufacturer can not afford the rejection of his finished product so often. Therefore, it is necessary to keep constant vigil on the quality of the finished product. For instance, the ball bearing is exactly circular and of a specified diameter, the size of the bolt is 5 cms exactly, each match box contains 50 sticks, a battery cell gives vurrent at 2 volts etc. These objectives can be fulfilled by the statiscal technique named statiscal quality control (SQC). With the aid of statiscal methods we can find out whether the variation in the articles is of a random nature, or whether some reason can be assigned for this variation. Thus, statistical quality control methods are applied to two phases of the manufacturing process.
- A control is to be maintained during the process of manufacturing of the articles.
- The secand phase is the checking of the quality of the manufactured product in respect of its acceptiblity
(Basic Statistics, B.L. Agarwall, 2006, pp. 585-586)
3)Non-Destructive Testing: [Test methods]
[Old]
Non-destructive testing is the evaluation of engineering materials without impairing their usefullness. As with the fracture mechanics, nondestructive testing can serve to analyze an existing failure or be used to prevent future failures. The techniques of this field are:
1. X-radiography testing,
2. Ultrasonics,
3. Eddy-current testing,
4. Magnetic particle testing,
5. Liquid penetrant testing,
6. Acoustic-emission testing.
(Shackelford J.F., Introduction to materials science for engineers, 4th Edition, p. 560, 562-564)
2. Ultrasonics,
3. Eddy-current testing,
4. Magnetic particle testing,
5. Liquid penetrant testing,
6. Acoustic-emission testing.
(Shackelford J.F., Introduction to materials science for engineers, 4th Edition, p. 560, 562-564)
[New][Better]
Flaws and cracks can play havoc with the performance of structures, so that the detection of deffects in solids is an essential part of quality control of engineering systems for their safe and successful use in pratical stuations. This is known variously as non-destructive testing (NDT). Quality control, quality technology, and noncontact measurements are related subjects that include or use NDT tecniques. However, applications of NDT go much deeper an are much broader inscope than the detection of gross defects. They concern all asoects of the characterization of solids,their microstructure, texture, morphology, chemical constituents, physical and chemical properties, as well as their methods of preparation. There is concern for the most minute detail that may affact the future performance of the object in service, so that all properties need to be under control and all factors understood that may lead to breakdown. Nor is it appropriate to rely on general statements because each study and each example needs to be treaded individually, proceeding by the use of all known properties and information about the component. The abbreviation NDT will be used in this text for "non-destructive testing".
A description of early evolution of NDT is given by Mullins and his review still covers most of the methods presently used. The established test methods include radiography, ultrasonics inspection, magnetic particle inspection, liquid penetrant inspection, thermography, electrical and magnetic methods, am visual-optical testing.
(Nondestructive testing: radiography, ultrasonics, liquid penetrant, magnetic particle, eddy current, Louis Cartz,1995,p. 1)
4)Smart Sensors [Group: Control Element]
[Old]
These sensors have the capability to perform a logic function, to conduct two-way communication, and to make decisions and take appropriate actions. The necessary input and the knowledge required to make a decision can be built into a smart sensor. For example a computer chip with sensors can be programmed to turn a machine tool off when a cutting tool fails. Likewise, a smart sensor can stop a mobile robot or a robot arm from accidentally coming in contact with an object or people by sensing quantities such as distance, heat, and noise.
(Kalpakjian S., Schmid S.R., Manufacturing engineering and technology, p. 1175)
[New][Better]
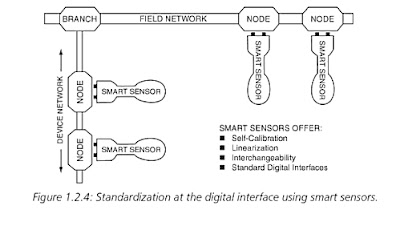
Digital techniques have become increasingly popular in processing sensor outputs in data acquisition, process control, and measurement. Generally, 8-bit microcontrollers have sufficient speed and proccessing capability for most applications. By including the A/D conversion and the micro controller programmability on the sensor itself, a "smart sensor" can be implemented with self- contained calibration and linearization features, among others. A smart sensor can then interface directly to an industrial network as shown in figure 1.2.4.
(Sensor technology handbook, 1. cilt,Jon S. Wilson, 2005, pp.19-20)
5)Boundary Representation (B-rep):[Group:design technique]
[Old]
[Old]
The boundary representation (B-rep) method is an extension of wireframe modeling in that the former includes the details of involved surface patches. A popular scheme employed is the Baumgart’s winged edge data structure for representation of solids. Though developed for polyhedrons, the Baumgart’s method is applicable to homeomorphic solids. That is, the primary B-rep data structure of a tetrahedron would be the same as that of a sphere over which a tetrahedron with curved edges is drawn. The difference would be that for a sphere, the edges and faces would be recorded as entities with finite curvature. The associated Euler-Poincaré formula is discussed next which is a topological result that ensures the validity of a wide range of polyhedral solids. Based on the Euler-Poincaré formula are the Euler operators for construction of polyhedral solids. Two groups of Euler operators are put to use, the MAKE and KILL groups for adding and deleting respectively. Euler operators are written as Mxyz or Kxyz for the Make and Kill groups respectively where x, y and z represent a vertex, edge, face, loop, shell or genus. Using Euler operators, every topologically valid polyhedron can be constructed from an initial polyhedron by a finite sequence of operations.
(Saxena A.,Sahay B.,Computer Aided Engineering Design,page.11)
(Saxena A.,Sahay B.,Computer Aided Engineering Design,page.11)
[New][Better]
Boundary Represeentation, or B-rep for short, can be considered as an extension to the wireframe model. The merit of a B-rep is that a solid is bounded by its surface and has its interior and exterior. The surface of a solid consists of a set of well-organized faces, each of edges that are curve segments. Therefore, a B-rep is an extension to the wireframe model by adding face information to the latter.
There are two types of information in a B-rep: topological and geometric. Topological information provide the relationships among vertices, edges and faces similar to that used in a wireframe model. In addition to connectivity, topological information also include orientation of edges and faces. Geometric information are usually equations of the edges and faces.
The orientation of each face is important. Normally, a face is sorrounded by a set of vertices. Using the right-handed rule , the ordering of these vertices for describing a particular face must guarantee that the normal vector of that face is pointing to the exterior of the solid. Normally, the order is counterclockwise. If that face is given by an equation, the equation must be rewritten so that the normal vector at every point on the part that is being used as a face points to the exterior of the solid. Therefore, by inspecting normal vectors one can immediately tell the inside and outside of a solid under B-rep. This orientation must be done for all faces.
The figure 9.2 shows three faces and their outward pointing normal vectors. To describe the top surface, the vertices should be 6, 7, 2, 1 or 7, 2, 1, 6 or 2, 1, 6, 7 or 1, 6, 7, 2. To describe the left face, the order shpuld be 1, 2, 3, 4 or 2, 3, 4, 1 or 3, 4, 1, 2 or 4, 1, 2, 3. Unfortunately not all surfaces can be oriented this way. If the surface of a solid can be oriented this way, it is called orientable, otherwise, it is non-orientable.
(Computer Graphics, Chennakesava R. Alavala,2009, p. 192)


No comments:
Post a Comment